Hallo, darf ich dir meine Freundin die Schnecke vorstellen? Heute sehen wir uns an, wie die Natur ein so schönes Haus wachsen lassen kann.

Hallo, ich bin Sparky. Ich bin total stolz auf mein schönes Haus. Siehst du wie toll es sich kringelt?

Auch in der Natur funktioniert vieles mit Mathematik. Die Kringel des Schneckenhauses kann man mit Zahlen und Mathematik beschreiben.

Zu diesem Beitrag benötigst du folgendes Material

• (kariertes) A4-Papier
• Bleistift / Farbstifte
• Lineal

Möchtest du auch ein Schneckenhaus zeichnen?

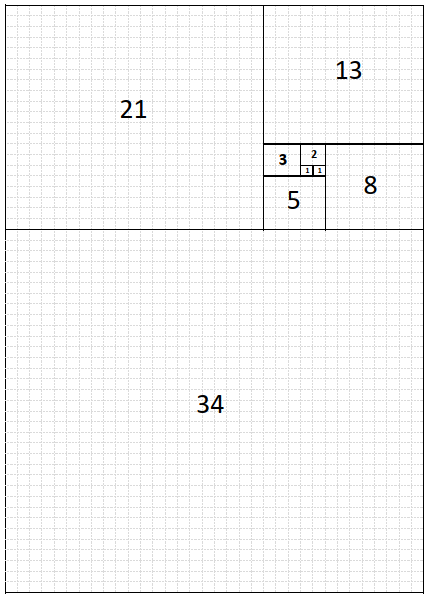
Zeichne dir auf ein Blatt (kariertem) Papier das Muster, das du auf der linken Seite am Bild siehst.

Die Zahlen in den Kästchen zeigen dir die Breite und die Länge des jeweiligen Quadrats.

Tipp: Das hier gezeichnete Muster kann auf einem kariertem A4-Blatt gezeichnet werden. Den Rand kannst du dann noch abschneiden.

Dann beginnst du beim linken kleinsten Quadrats mit der Zahl 1 und zeichnest einen von der linken oberen Ecke eine gebogene Linie (Viertelkreis) zur rechten unteren Ecke. Von dort zeichnest du wieder eine gebogene Linie im nächsten Quadrat usw.

Wenn du mit deiner Linie an der Ecke rechts ganz unten in deiner Vorlage angekommen bist, dann ist dein Schneckenhaus fertig.

Du kannst dir aber auch die Vorlagen hier herunterladen

Vorlage mit Raster und Zahlen

Vorlage mit Raster und Hilfslinie

Vorlage nur Raster ohne Zahlen

Vorlage Ergebnis Schneckenhaus

Bilder: © Günther Lehner

Zusatzwissen

Die Zahlen in den Quadraten deines Schneckenhauses werden als Fibonacci-Zahlen bezeichnet. Benannt ist die Reihe von Zahlen (=Folge) nach Leonardo Fibonacci, also Fibonacci-Folge.

Er berechnete damit bereits im Jahr 1202 das Wachstum der Hasenpopulation.

Weitere Untersuchungen ergaben, dass durch diese Zahlenfolge noch weitere Wachstumsvorgänge in der Natur beschrieben werden können – die Folge ist also eine Art Wachstumsmuster der Natur.

Die Fibonacci-Folge f₁, f₂, f₃,… ist durch folgendes Bildungsgesetz definiert:

f_n = f_n-1 + f_n-2 für n >= 3

und den Anfangswerten

f₁ = f₂ = 1

Die Fibonacci-Folge ist eine unendliche Folge natürlicher Zahlen.

Das bedeutet in Worten:

Für die beiden ersten Zahlen wird der Wert 1 vorgegeben.
Jede weitere Zahl ist die Summe ihrer beiden Vorgänger in der Folge.

Hier kannst du dir ansehen, wie sie berechnet werden.

• 1
• 1
• 1 + 1 = 2
• 1 + 2 = 3
• 2 + 3 = 5
• 3 + 5 = 8
• 5 + 8 = 13
• 8 +13 = 21

also:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…

Günther

ideenspielraum